弧度法の優位性・利便性

弧度法は、三角関数のグラフをかくときにその存在価値を発揮します。

y=sinxのグラフは、形は決まっていますから、基本的に５つの点を取ればかけますね。

５つの点は、弧度法と度数法ではそれぞれ、

　度数法・・・　0° , 90° , 180° , 270° , 360°

　弧度法・・・　0 , π/2 , π , 3π/2 , 2π

です。

実際にグラフをかくとなると、

度数法では、メモリが必要になります。しかし、弧度法にはメモリは必要ありません。　　【図1,2】

なぜなら、周期である2πを４等分すれば取れるからです。周期2πを半分、半分に切っていけばよいのだから。

すなわち、点の取り方としては、まずは、0と2πのふたつ、そしてその半分（中点）であるπ、さらに半分にする（中点を取る）とπ/2と3π/2がとれます。　【図３】

y=sin2xのグラフならされにその便利さが分かります。周期はπですから。

すなわち、0とπのふたつ、そしてその半分（中点）であるπ/2、さらに半分にする（中点を取る）とπ/4と3π/4がとれます。　【図３】

目盛はなくて大丈夫ですね。必要なら、後からつければよいですね。どちらも、図３でかけます。

グラフ用紙を用意してみました。

図1

図2

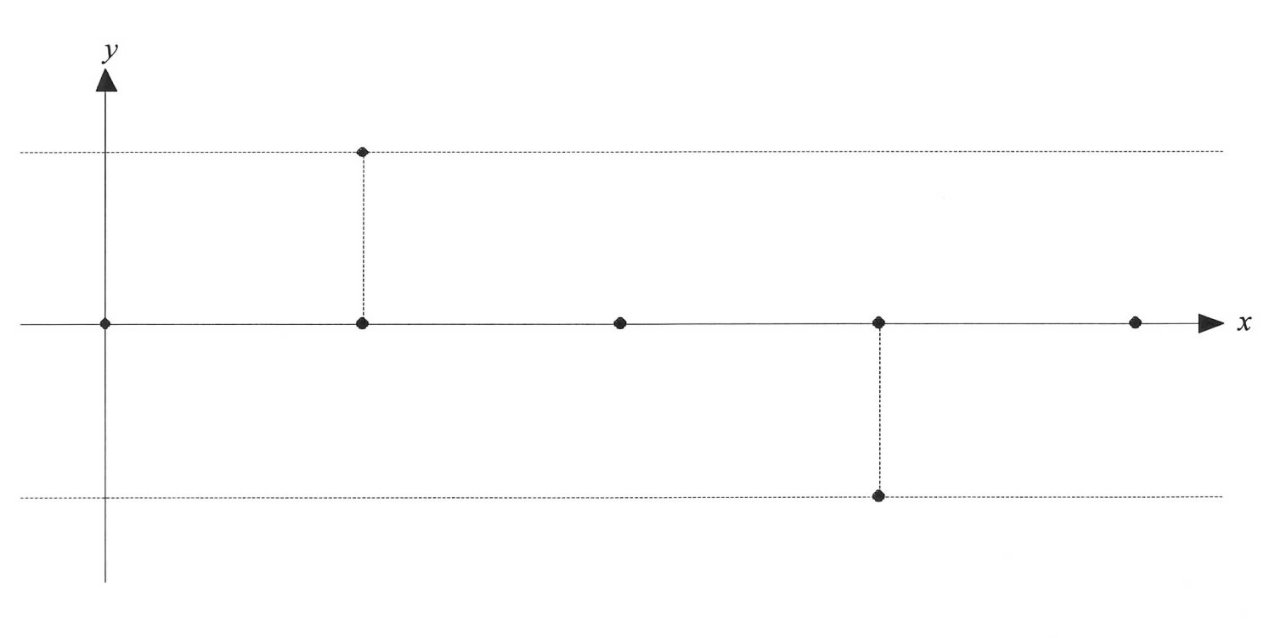図３

このように、弧度法は、πを基準としてそれを分数を使ってあらわすので、目盛なしでグラフがかける訳です。

別の、項目でも述べますが、グラフはかくことよりも、使えることが大事ですから、三角関数のグラフがササッとかける弧度法は非常に便利ですね。